Abstract
This paper presents maps of the inferred relative prevalence of PD in England. The maps are based on data from publicly accessible data sets:
- one that contains for each of the 10,000 GP practices in England the number of NHS prescriptions written for each drug in June 2012;
- one that shows the post code of each practice;
- one that shows the eastings and northings of each post code.
The data does not explicitly mention PD, so we adopt a proxy measure. This is based on the observation that some drugs, such as levodopa, are associated with PD. The ratio between the number of "Parkinson's" prescriptions written by a practice and the total number of prescriptions that it writes gives an indication of the prevalence of PD in that practice's catchment areas. We go one stage further, we derive our proxy measure by dividing a practice's ratio by the national average ratio. This gives the inferred relative prevalence for that practice. It is from these values that the maps are drawn.
The need for the work
Finding variations in the prevalence of Parkinson's Disease is of interest for a number of reasons. They may give clues as to:
- the aetiology of the disease;
- the effectiveness of various therapies;
- what environmental toxins are involved in PD.
In short, if we understood the spatial differences in PD's prevalence, we would be much closer to finding a cure.
As far as I'm aware, there are only two papers that give detailed maps of prevalence across a whole country. One by Willis et al. [1] for the US. And one by Pedro-Cuesta et al. [2] for Spain. I've found nothing similar for the UK. It is this gap, at least as far as England is concerned, that this paper hopes to go some way to address.
Data
The UK government through its Open Data initiative [3] has now made it easy to, at least, make a start on filling this gap. Amongst the many data sets that are open to the public are ones relating to prescriptions. Personal details such as the names of the people to whom the prescriptions are written are not disclosed.
The maps are based on NHS prescription data from June, 2012, from each of about 10,000 GP's surgeries in England. Some of the maps are based on the whole sample. Some, where appropriate to avoid distortion by unrepresentative smaller practices, are based on a reduced sample of 8400 that comes from including only those practices that wrote at least 500 prescriptions in the month. The distribution of practices is felt to reasonably follow that of the population.
For this work I've used three data sets:
- Raw data for June 2012, from file T201206PDPIEXT.CSV, obtained from [4], giving: "All prescribed and dispensed medicines (by chemical name), dressings and appliances (at section level) are listed for each GP practice. -For each GP practice, the total number of items that were prescribed and then dispensed is shown. -The total Net Ingredient Cost and the total Actual Cost of these items is shown."
- Raw data for June 2012, from file T201206ADDREXT.CSV obtained from [4], giving addresses including, importantly, postcode.
- Positional data from the Ordnace Survey, Code-Point data set [5]. This gives Easting and Northing information for each postcode.
A critical feature of the analysis is the identification of "Parkinson's" drugs. These were taken to be those drugs with BNF numbers from 0409010A0 to 0409020S0. See Table 1.
Inferred relative prevalence
The data makes no explicit mention of Parkinson's disease. So, the crucial question is: How do we extract PD prevalence data?
Strictly speaking, we don't. Instead, we look for a weaker measure: relative prevalence. This allows us, in this context, to answer questions like, Where in England is PD most common?. But not, how many people in England have PD?
So, we're looking for a measure of relative PD prevalence. That's not in the database either. A proxy is used:
| NUMBER PARKINSON'S PRESCRIPTIONS | |
| INFERRED RELATIVE PREVALENCE (IRP) = | -------------------------------------------------- |
| TOTAL NUMBER PRESCRIPTIONS |
First we argue for the use of IRP for an individual practice. Although exceptions can be found to each of the following claims, we argue that regardless of the prescribing policies and patient mix of a practice the following statements are stochastically correct, (in the sense that each is an unbiased estimator of the true situation):
- more Parkinson's prescriptions implies more PD patients;
- more PD patients implies more PD prescriptions;
- the number of Parkinson's prescriptions has a linear relationship with the number of patients with PD.
Secondly, we argue that aggregating the results from a group of practices by aggregating the raw data gives an unbiased estimator of the overall situation.
Limitations of this approach
Does the approach adopted here give results exactly equivalent to the true rate of PD prevalence? Of course not, for instance:
- PwP not on prescription drugs are missed entirely;
- doctors who prescribe two different drugs, rather than double the quantity of a single drug will get twice the inferred prevalence;
- doctors who prescribe small quantities, e.g. a week's supply rather than a month's, on each prescription will have higher rates;
- different local prescribing regimes will lead to differing inferred rates;
- demographics, like age profile, are missed;
- specializations, such as a focus on nursing home patients is missed;
- changes in the use of non-Parkinson drugs at place A will impact on the relative inferred rate at place B.
- some of the Parkinson drugs can be used for other conditions, etc..
- patients don't necessarily live close to the practice surgery.
A deeper problem is that with a slowly progressing disease such as Parkinson's a patient may have lived in many areas during the course of the illness. So, even if the identification of the disease by the prescription method is correct, any attempt to use the IRP statistics, such as to find spatial correlations with environmental toxins, is made harder.
But, although these problems will certainly add noise to the statistics, I don't think they will invalidate the whole approach.
Analysis
And the results? It is early days yet, but some things can be seen:
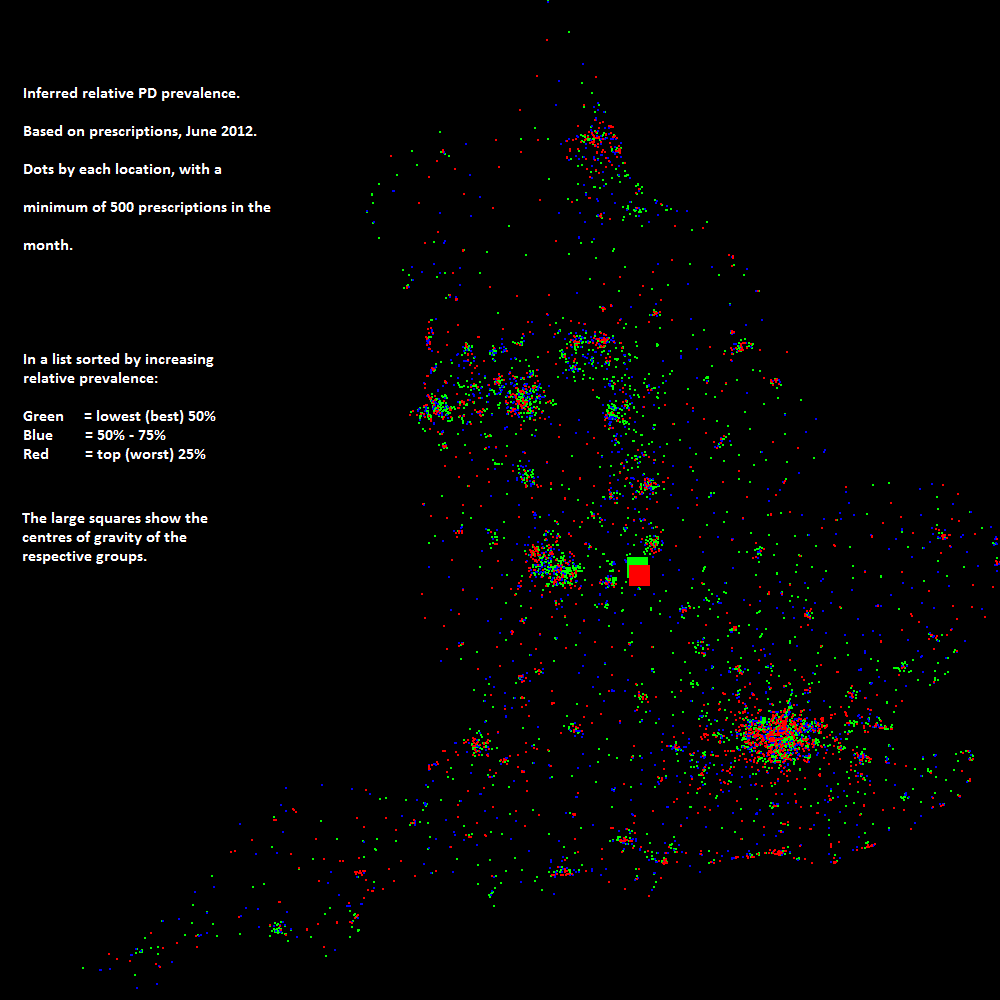
Plotting the whole sample does not show large regional differences like those reported in the US. The most telling measure of this, albeit not a sufficient condition to disprove large variances in distribution, is that the "centres of gravity" of the source of all prescriptions compared with the PD prescriptions differ by only a few miles. See Map 1.
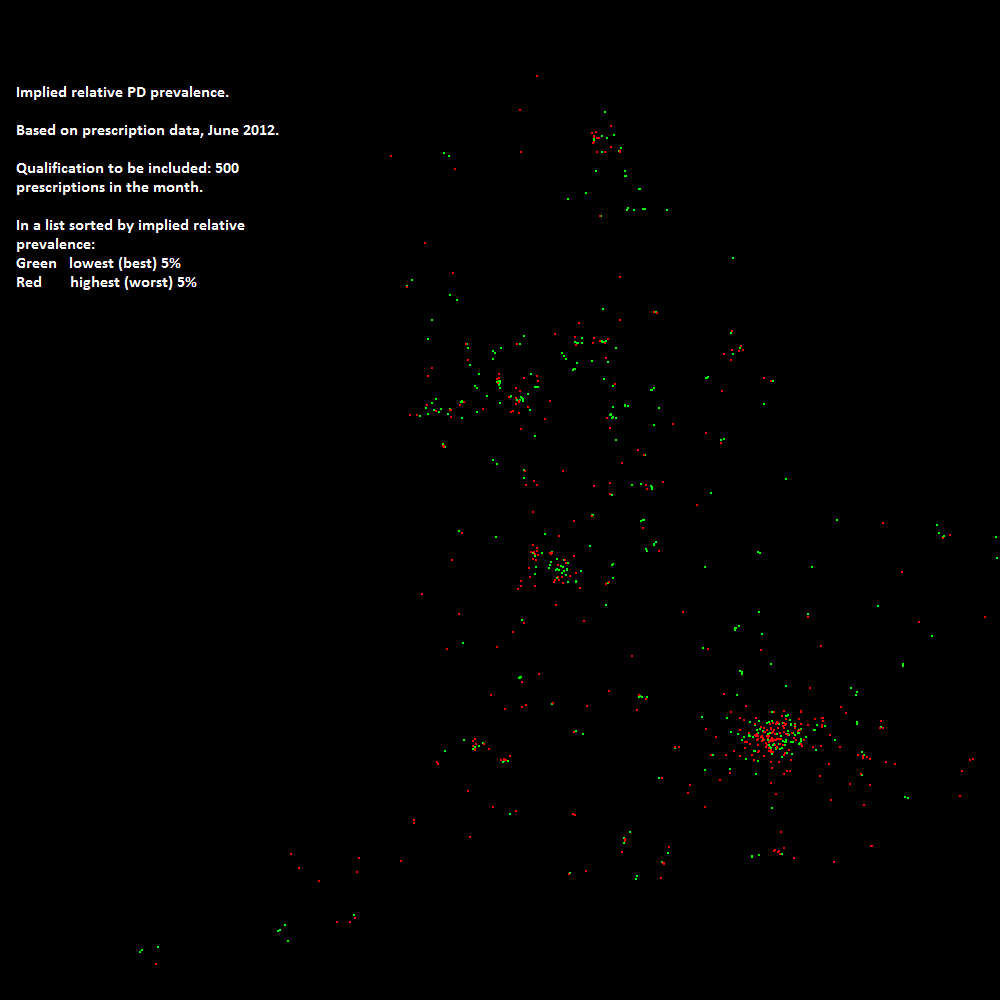
However, analyses based on on comparisons between the lowest and highest prevalence practices hint at spatial variations. For instance, Map 2 shows the bottom 5% and the top 5% of practices ordered by inferred rates, hint at variations, with the South West appearing to have higher prevalence rates. This may just reflect demographics.
Data attribution
The main condition for the use of the data sets is that you attribute the source, which in this case is:
- Contains Ordnance Survey data © Crown copyright and database right [2012]
- Contains Royal Mail data © Royal Mail copyright and database right [2012]
- Contains National Statistics data © Crown copyright and database right [2012]
Provided you do this the Open Government Licence gives you the right to use, distribute and adapt the data.
References
[1] "Geographic and Ethnic Variation in Parkinson Disease: A Population-Based Study of US Medicare Beneficiaries"
Allison Wright Willis, Bradley A. Evanoff, Min Lian, Susan R. and Brad A. Racette
Neuroepidemiology. 2010 April; 34(3): 143–151.
http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2865395/
[2]"Spatial distribution of Parkinson's disease mortality in Spain, 1989-1998, as a guide for focused aetiological research or health-care intervention"
Jesús de Pedro-Cuesta, Eduard Rodríguez-Farré and Gonzalo Lopez-Abente
BMC Public Health, vol 9, Dec 2009.
http://www.biomedcentral.com/1471-2458/9/445
[3] http://data.gov.uk/
[4] http://data.gov.uk/dataset/gp-practice-prescribing-data
[5] http://www.ordnancesurvey.co.uk/oswebsite/products/code-point/index.html
[6] http://neurotalk.psychcentral.com/thread179755.html
John
| Drug Code | Drug Name | Total items | NIC | Actual cost |
| TOTAL | TOTAL | 78609510 | 658805467 | 609262986 |
| including | ||||
| 0409010A0 | Apomorphine Hydrochloride | 935 | 567602 | 522883 |
| 0409010B0 | Amantadine Hydrochloride | 8833 | 81237 | 75085 |
| 0409010H0 | Ropinirole Hydrochloride | 38929 | 1045358 | 964080 |
| 0409010I0 | Levodopa | 2 | 206 | 190 |
| 0409010K0 | Co-Beneldopa (Benserazide/Levodopa) | 58354 | 369203 | 341836 |
| 0409010N0 | Co-Careldopa (Carbidopa/Levodopa) | 69102 | 1017974 | 939828 |
| 0409010P0 | Pergolide Mesilate | 293 | 12049 | 11108 |
| 0409010S0 | Tolcapone | 123 | 10450 | 9630 |
| 0409010T0 | Selegiline Hydrochloride | 4334 | 54446 | 50280 |
| 0409010U0 | Cabergoline | 651 | 72850 | 67125 |
| 0409010V0 | Entacapone | 4344 | 228720 | 210818 |
| 0409010W0 | Pramipexole | 26646 | 1466118 | 1351319 |
| 0409010X0 | Levodopa/Carbidopa/Entacapone | 14663 | 960851 | 885533 |
| 0409010Y0 | Rasagiline Mesilate | 9484 | 723728 | 666954 |
| 0409010Z0 | Rotigotine | 5756 | 748280 | 689465 |
| 0409020C0 | Trihexyphenidyl Hydrochloride | 7742 | 83730 | 77368 |
| 0409020E0 | Benzatropine Mesilate | 39 | 1914 | 1764 |
| 0409020N0 | Orphenadrine Hydrochloride | 5996 | 194940 | 179758 |
| 0409020S0 | Procyclidine Hydrochloride | 65514 | 210941 | 1964037 |
| PDTOTAL | PDTOTAL | 321740 | 7850604 | 7241436 |
Table 1: list of "Parkinson's" drugs, prescriptions, June 2012.